这个数据为王的时代,我们缺乏的不是数据、工具、算法,而是数据思维。

最近在学习「数据分析思维」,这里总结了12个常见数据分析的理论/悖论,分享给你。
1、辛普森悖论
2、大数定律
3、小数陷阱
4、墨菲定律
5、幸存者偏差
6、帕累托法则
7、马太效应
8、正太分布
9、拉普拉斯分布
10、德克萨斯神枪手谬误
11、因果倒置
12、柏克松悖论
让数据,给你一双看透本质的眼睛。
辛普森悖论是指,在分组比较中都占优势的一方,在总评中有时反而是失势的一方。
比如这个表中,两分球和三分球投中率都比球员A高的球员 B,整体的命中率反比球员A低。
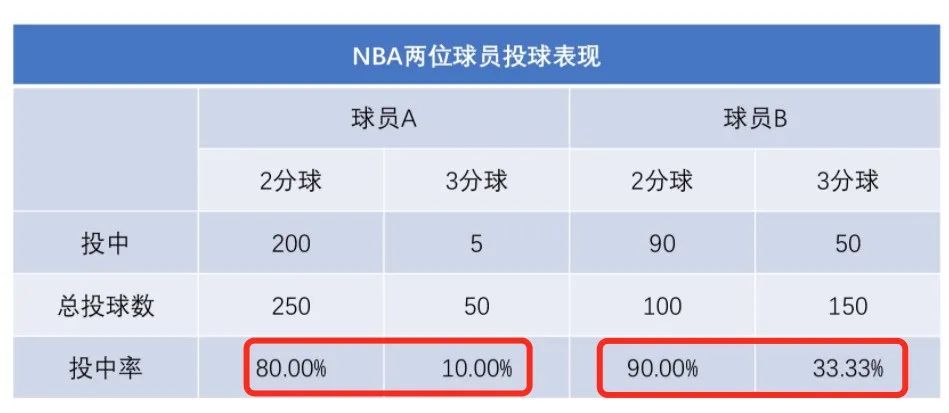
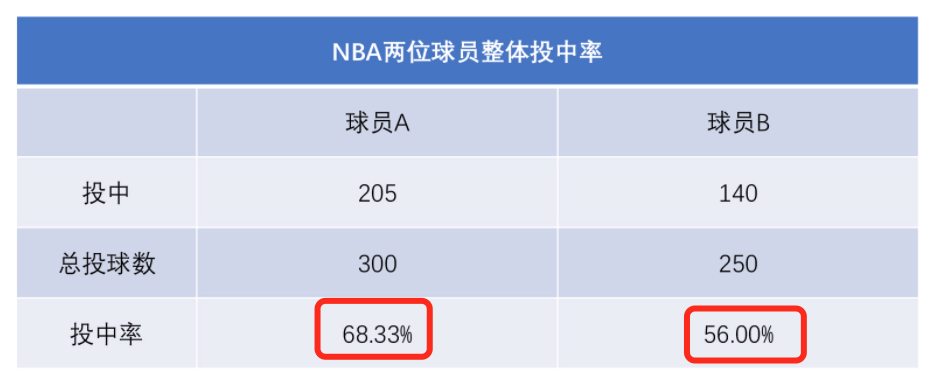
也就是说,“质”(命中率)与“量”(投球数)是两个维度的数据,如果全部合并成“质”(命中率)这个维度的数据,那就会出错。
大数定律是指,当随机事件发生的次数足够多时,发生的频率才会趋近于预期的概率。
随机抛硬币,出现正面和反面的概率均为 50%,也就是一半正面一半反面。
但如果你抛10次,可能7次正面3次反面,或者8次正面2次反面,并不是5次正面5次反面。
只有你当你抛几千次、几万次时,正面和反面的概率,才趋近于50%。
小数陷阱,也叫赌徒谬误,比如去赌场玩俄罗斯轮盘,连续 10 次开小了,你心里可能会觉得连续 10 次小了,下一次开大的概率更高一些,然后就去押大。这是典型的“赌徒谬误”,是错误的。
每次开大还是开小,是独立且随机的,并不是前面都是“大”,后面开“小”的概率就会高。
大数定律里面,最重要的是“大数”,也就是说你得出现足够多的次数,才能够趋近于它的期望概率。一般的赌徒都没有赌到足够多的时候就已经输成穷光蛋了。
赌场其实是在利用大数定律赚钱,一般的赌博机都会被设计成为 51% 比 49% 的这种预期概率,赌场其实只赢 2%,而你却会输 100%。
总之你越不希望某件事情发生,这件事情往往就会发生,怕什么来什么。这就是墨菲定律。
紧急赶时间,恰好每个路口都遇到红灯。
上班时工作较少,下班时恰好来活。
不打车时街上到处都是空出租车,但等你需要打车时发现全是满员的。
...
其实墨菲定律不是一个数学规律,而是一种选择性记忆的心理学现象。
顺利的事情,不会令人记忆深刻,只有那些让人感到愤怒、挫败和痛苦的记忆,最难磨灭。
如果用数据分析的思维去看墨菲定律,这是一个期望值的问题,是我们对于好事情和坏事情的期望值差异造成的。
幸存者偏差是指,当取得资讯的渠道仅来自幸存者时,我们得出的结论可能会与实际情况存在巨大偏差。
幸存者偏差这个概念来源于二战时期,战争中,战机机身上几乎所有地方都可能中弹,因此需要用统计学研究战机被击中的部位,从而确定哪个部分需要额外加强装甲。
人们对返航的战机进行弹痕分析后发现,飞机机翼和尾部被打穿的弹孔较多,由此得出应该是加强机翼的装甲防护会更好。
但对返航的飞机样本来说,其实是说明即使机翼中弹,飞机也有很大的几率能够返航。对于那些弹孔不多的部位来说(比如驾驶舱、油箱和机尾),当这些部位中弹的时候,飞机很可能连飞回来的机会都没有了,而这并没有统计出来,这就是所谓的“看不见的弹痕最为致命”。
最后事实也证明,加强弹孔较少部位的装甲防护是正确的。
帕累托法则,也叫做二八法则,简单来说,就是 20% 的人占了 80% 的资源,剩下 80% 的人分最后 20% 的资源。这个法则诞生于帕累托的花园。有一天帕累托偶然发现,自己园子里绝大部分的豌豆是由园子里极少部分豌豆荚产生。
这样的规律其实无处不在。
语言中常用词只有500-1000个,剩余的更多词汇使用很少。
20%的员工,为公司做出了80%的业绩。
20%的人,掌握了全世界80%以上的财富。
...
那么这种现象是怎么产生的呢?
病毒、树种和语言其实都有一个共性——传播性。比如在亚马逊雨林里,两株植物长在了一块,那么每天这两株植物就要为阳光和土壤中的养分去竞争。如果其中一株能比另外一株植物每天稍微长快一点,那么它就能长得更高,从而获得更多的阳光、吸收更多的养分。如果每天都有这些额外的能量,这株植物就更加有能力把种子给传播出去,然后复制这种模式。一直持续下去,这种植物就会积累出得天独厚的优势。
开始的微妙的优势会随着时间逐步加强,最后就能占领绝对优势,就像滚雪球一样,越滚越大。
马太效应是指,大者恒大,赢家通吃。马太效应来源于圣经《新约·马太福音》,文中是这样描述的:“ 凡有的,还要加给他,叫他多余。没有的,连他所有的也要夺过来 ”。
比如电商平台,用户越多,入驻的商家就越多;商家越多,提供的商品越丰富,用户就越多。原来属于小电商平台的用户和商家,都都会逐步来来到大的电商平台。
马太效应告诉我们,我们身处的世界是赢者通吃的世界,开始时细微优势最终将带来无穷多的回报。反之,最初的细微劣势也将导致最终一无所有。
正态分布也叫高斯分布,就是你在课本里曾经学过的那个两头低、中间高然后左右轴对称的钟形曲线。
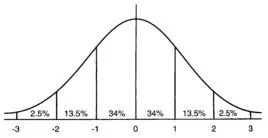
学术上是这么来定义正态分布的:“如果一个量是由许多微小的独立随机因素影响的结果,那么就可以认为这个量具有正态分布”。听完这个定义,是不是有点懵,拿个示例来说。
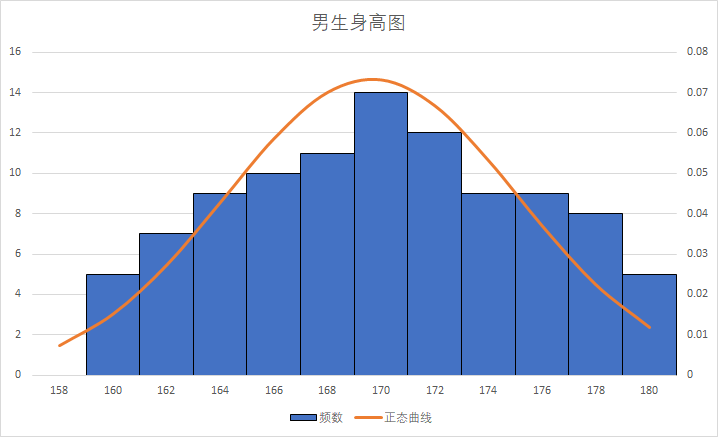
比如我们知道中国人的平均身高大概是 1 米 7,那么实际上我们随机找 100 个人,把每个区间的身高累个计数画出来一个直方图,它就会是一个正态曲线。
拉普拉斯分布,是一个“凸”字形的塔尖儿曲线,从左到右,斜率先缓慢增大再快速增大,到达最高点后变为负值继续先快速减小,最后再缓慢地减小,所以有点像“往里边凹陷的金字塔”。
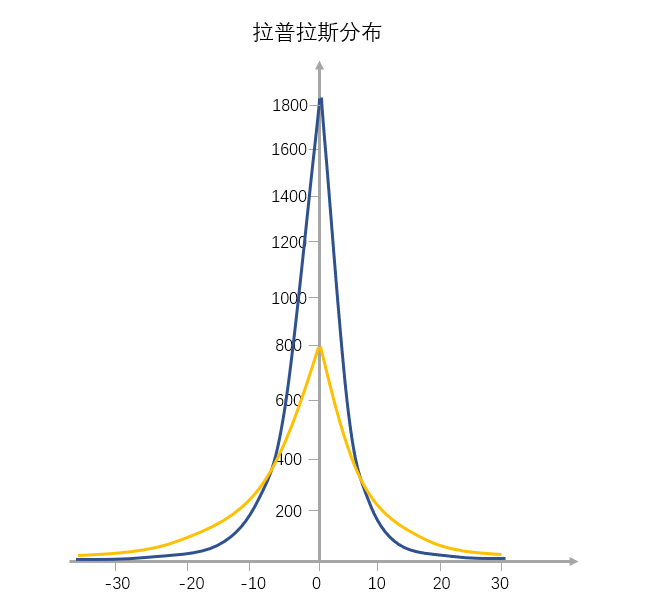
对比正态分布图像,我们可以看到拉普拉斯分布图像是尖峰厚尾的,塔尖上的那些,就是我们看到的稀缺资源。
比如说房价,理论上房价应该和人的身高一样,在某一个地区有一个均价,并且整体的房价和身高是一样呈正态分布。但为什么在某一个区域可能就隔了一条街,房价却翻了好几倍,而且数量也不少?
在信息透明和市场竞争的情况下,房价、工资、股票都会符合一个特点:越塔尖的个体越具有资源吸附能力。
先有弹孔,还是先有靶子。
当年在美国西部得克萨斯州发现一个神枪手,他经常在各地的民居的墙上练习射击,几乎他所有的弹孔都集中在十环左右这个中心的区域。他已经成为了神话,人们一直在寻找他。
但是当人们真的找到了这个神枪手后,发现他自己打枪其实一点都不准,也不敢跟其他人去决斗。
那他墙上的这些靶子和枪手点是怎么形成的呢?原来他是先朝墙上开很多枪,然后在弹孔最密集的地方画上了十环的靶子,再把散布在其它地方的弹孔用原来的泥土补起来。这样看上去,他每个地方打的靶子都很准确,因为先有弹孔,再有靶子。
这就是德克萨斯神枪手谬误。
在我们日常生活当中也很容易出现这种情况,当你看到一个数据散点报告的时候,你一定要看清背后所蕴含的实际数据是不是涵盖了所有的数据,还是只给你看了最有这种数据规律的数据。前者就像先有靶子来瞄准再去射击,后者就好比先射击完最后再画上靶子,这样结果会完全不同。
典型的因果倒置就是,天亮了鸡就开始打鸣,但是我们不能说是因为鸡打鸣导致了天亮。
但是实际的应用当中,我们往往会忽略这个逻辑。
比如,我们在一些医学统计上会看到说不吃早饭会导致人肥胖,甚至还有大量的统计数据表明这些肥胖的人都没有吃早饭。
问题是,数据的确是同步发生的,但是不代表这些数据之间有因果关系。而且有可能会出现因果倒置——肥胖的人胖所以早上不饿,所以他不吃早饭。而比较瘦的人自身代谢比较快,晚上消耗多,早上就会比较饿,所以他要吃早饭。
伯克松悖论是指,当不同个体被纳入研究样本的机会不同时,研究样本中的两个变量 X 和 Y 表现出统计相关,而总体中 X 和 Y 却不存在这种相关性。听上去是不是有点拗口?没关系,我们看个例子。
比如“海军与平民死亡率”的例子。在 1898 年“美西战争” 期间,美国海军的死亡率是 9%,而同期纽约市市民的死亡率为 16%。后来海军征兵部门就拿这个数据跟大家讲,待在部队里其实比大家待在家中更加安全。
这逻辑肯定是错误的,但错误不在具体数据,而是这两组数据其实没有什么可比性。
因为海军的主要是年轻人,他们身强体壮、不会出现太多身体疾病;而纽约市民里面包含了新出生的婴儿、老年人、病人等等,这些人无论放在哪里,他的死亡率都会高于普通人。
这是数据分析中非常常见的几个理论,也能用来解释生活中诸多现象。
数据,给你一双看透本质的眼睛。
学完这12个理论,恭喜你,又多了一个看清世界的思维。